Warnhinweise bei Schuleintritt

Risiko für „Rechenschwäche“ bei SchulanfängerInnen – FRÜHERKENNUNG UND GEGENMASSNAHMEN

Autor: Michael Gaidoschik

Die folgenden Ausführungen sollen LehrerInnen in den ersten Wochen und Monaten der ersten Schulstufe dabei helfen, möglichst frühzeitig zu erkennen, ob einzelne Kinder der Klasse ein erhöhtes Risiko für die Entwicklung einer „Rechenschwäche“ tragen, und vor allem: Sie sollen dabei helfen, geeignete Fördermaßnahmen in die Wege zu leiten.

Voraussetzung dafür ist eine Unterrichtsgestaltung, die gerade in der Eingangsphase das Anregen und möglichst individuelle Beobachten in den Vordergrund stellt. Über die Schwierigkeiten einer Umsetzung in Klassen von bis zu 25 Kindern mit unterschiedlichsten Lernvoraussetzungen sind wir uns schmerzlich bewusst. Wir wünsche Ihnen und den von Ihnen betreuten Kindern, dass Sie es dennoch zumindest ansatzweise schaffen!

Defizite im Bereich des Zählens    

• Zählen ohne Anzahlbewusstsein
  Wenn ein Kind auf die Frage „Wie viele sind das?“ so reagiert, dass es die Elemente einer Menge nacheinander antippt und dabei die Zahlwortreihe „eins, zwei, drei …“ hochgeht, dann sollte das nicht ohne weiteres schon als „Beweis“ dafür genommen werden, dass das Kind Zahlen als Anzahlen denkt. Tatsächlich beginnen manche Kinder, die gerade eine Menge in dieser Weise ausgezählt haben, sofort aufs Neue zu zählen, wenn man nachfragt: „Und, wie viele sind es jetzt?“ Manche zählen etwa auch die Finger einer Hand bei jeder „Wie viel?“ – Frage immer wieder aufs Neue ab; das Zählergebnis „fünf“ wird von ihnen offenbar nicht als feststehende Anzahl verstanden und festgehalten. Offenbar verstehen manche Kinder die Frage nur als Aufforderung, die (gewusste) Zahlwortreihe von eins beginnend aufzusagen.
• Zählen ohne Eins-zu-Eins-Zuordnung
  Manche Kinder missachten beim Zählen das „Eindeutigkeitsprinzip“ (vgl. Gelman/Gallistel), d.h.: Sie zählen ohne klare Eins-zu-eins-Zuordnung zwischen gesprochenem Zahlwort und jeweils angetippter Sache. Entweder der Finger eilt der Zunge davon; oder die Zunge dem Finger; mitunter gibt die Silbe „den Takt“ vor, was etwa zu Zählfehlern beim zweisilbigen sie-ben führt:

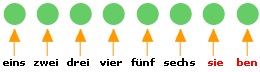Wesentlich für die richtige Beurteilung solcher Zählfehler: Fallen dem Kind selbst solche Fehler auf? Fällt es ihm beispielsweise als Unstimmigkeit auf, wenn beim wiederholten Auszählen ein und derselben Menge (aufgrund solcher Zählfehler) unterschiedliche Zählresultate herauskommen? Weiß es grundsätzlich sehr wohl, dass beim Zählen auf eine Eins-zu-Eins-Zuordnung zu achten wäre (und scheitert dabei aber immer wieder) – oder ist ihm dies eben tatsächlich gar nicht klar (weshalb es subjektiv auch gar keinen Fehler macht, wenn es bei sie-ben auf zwei Gegenstände deutet)?

• Defizite beim Weiterzählen
  Die Zahlwortreihe wird zu Schulbeginn von den meisten Kindern bis wenigstens zehn beherrscht (das ist jedenfalls empirischen Studien gemäß die Normalität).. Manche Kinder haben aber (aus unterschiedlichen Gründen) noch große Probleme damit, etwa von einer beliebigen Zahl ausgehend weiterzuzählen; sie müssen stets bei „eins“ anfangen, um beispielsweise die „Zahl nach vier“ zu ermitteln.
• Defizite beim Rückwärtszählen und Rückwärts-Weiterzählen
  Die umgekehrte Zahlwortreihe (zehn – neun – acht …) bereitet weit mehr Kindern noch zu Schulanfang Probleme als die Zahlwortreihe vorwärts. Folgeprobleme sind zu befürchten, wenn nicht frühzeitig nachgefördert werden kann.

Sinnvolle Maßnahmen zum Erarbeiten/Absichern des anzahlverständigen Zählens:

• Nicht dauernd, aber immer wieder: Kinder sollen beim Zählen einer Menge die gezählten Dinge nach jedem Schritt als Gesamtheit zusammenfassen („die alle zusammen sind fünf“, „das sind zusammen sechs“) – im Unterschied zum Antippen von nur jeweils einem Gegenstand beim Aussprechen eines Zahlwortes („fünf“ – getippt wird auf den fünften; „sechs“ – getippt wird auf den sechsten).
• Kinder sollen eine vorgegebene Anzahl von Gegenständen in eine verschließbare „Zählschachtel“ hinein zählen, diese verschließen, dann die Frage beantworten: „Wie viele sind jetzt drin?“ Die „Zählschachtel“ wird geschüttelt, danach erneut gefragt: „Wie viele sind jetzt drin?“ „Wenn Schütteln nichts daran ändert, wie viele es sind: Wodurch lässt sich das dann ändern?“ (Erhoffte Antwort: nur durch Dazugeben oder Wegnehmen! Wenn diese Antwort nicht kommt: Ausprobieren lassen! „Was musst du tun, damit es mehr werden? Was musst du tun, damit es weniger werden?“)
• Kinder sollen eine Reihe von Zähldingen von einer Seite beginnend zählen. Dann Frage: „Was ist, wenn du auf der anderen Seite zu zählen beginnst?“ Wenn Kind zählen will, soll es zählen, dann aber muss darüber gesprochen werden: „Wie war es vorher? Fällt dir etwas auf?“ Ziel: Das Kind erkennt, dass es beim Zählen nicht darauf ankommt, in welcher Reihenfolge die einzelnen Gegenstände erfasst werden. Wichtig ist nur, dass jeder Gegenstand genau einmal erfasst wird.
• Gezieltes Training des Weiterzählens von einer bestimmten Zahl aus, in Kombination mit dem Gedanken „um 1 mehr“: In der Zählschachtel sind schon fünf Würfel. Einer dazu – wie viele sind es jetzt? Usw.
• Dazu auch Zählen der eigenen Finger unter Betonung der Gesamtheit: Ein Finger ausgestreckt, „das ist ein Finger“; einer dazu, „jetzt sind es zwei Finger“; einer dazu, „jetzt sind es drei“, usw.
• Gezieltes Training der Zahlwortreihe rückwärts, einerseits als reine Wortreihe, andererseits in Kombination mit dem Gedanken „immer um eins weniger“. Beispielsweise auch in Kombination mit dem Darstellen der Zahlen bis zehn mit den eigenen Fingern: Zehn Finger ausstrecken, „das sind zehn“, einer weg, „jetzt neun“, wieder einer weg, „jetzt acht“, usw. Das bietet auch eine gute Gelegenheit für ein erstes Besprechen von „null“ als „gar keine Finger“.

Für alle diese Anregungen gilt:

Wenn Kinder (wie zu erwarten ist) die Zahlwortreihe schon bis wenigstens zehn beherrschen, dann sollte auch die Vertiefung und Absicherung des Verständnisses fürs Zählen (Bestimmen einer Anzahl) mindestens im gesamten Zahlenbereich bis wenigstens zehn erfolgen. Künstliche Begrenzungen des „Eingangs-Zahlenraumes“ (erst nur bis vier oder fünf), wie sie in vielen österreichischen Schulbüchern (im Gegensatz zu zeitgemäßen deutschen Lehrwerken) immer noch üblich sind, sind nicht nur, aber gerade auch für diesen Zweck geradezu schädlich! Vgl. dazu etwa Wittmann/Müller 1992, Scherer 1999, Gaidoschik 2003.

Defizite im Verständnis von „mehr“, „weniger“, „gleich viel“

• Anzahlvergleiche nach dem Augenschein
  Manche Kinder unterscheiden nicht ausreichend zwischen „gleich viel“ und „gleich lang“. „Mehr“ ist für sie immer das, was mehr ausschaut:

„Die unteren sind mehr, das sieht man doch!“
(Das so urteilende Kind verspürt keinen Zweifel, keine Veranlassung, genauer zu schauen, seinen ersten Eindruck zu überprüfen.)

 „Das sind gleich viele, sieht man doch, da und da (zeigt auf die hier mit einem roten Strich markierten Enden der beiden Reihen) ist’s gleich!“

• Anzahlvergleich ausschließlich durch Zählen
  Die meisten SchulanfängerInnen führen Anzahlvergleiche zählend durch. Daran ist nichts auszusetzen, doch gibt es bestimmte Anordnungen von Mengen, die weit ökonomischer durch Eins-zu-eins-Zuordnung verglichen werden können:

Kinder, die auch bei solchen Anordnungen meinen, zählen zu müssen, haben vielleicht noch nicht verstanden, dass „gleich viel“ (egal wie es ermittelt wird) nichts anderes heißt als: zwischen den Elementen zweier Anzahlen ist eine eindeutige Eins-zu-eins-Zuordnung möglich; jedes Element der einen Anzahl hat eine Entsprechung in der anderen Anzahl, nach erfolgter Zuordnung „bleibt keines übrig“.

Dasselbe trifft mit einiger Wahrscheinlichkeit für Kinder zu, die (siehe oben) „gleich viel“ nur nach dem Augenschein beurteilen. Ohne Verständnis von „gleich viel“ im Sinne einer Eins-zu-eins-Zuordnung (und ohne das entsprechende Verständnis von „mehr“ und „weniger“) ist ein tragfähiges Zahlverständnis aber nicht möglich. Eine erste mögliche Folgeschwierigkeit ist das

• Unverständnis gegenüber „um wie viel?“ – Aufgaben
  Manche Kinder können die Zahlwortreihe aufsagen, wissen auch, dass „sechs nach fünf“ kommt, sind aber ratlos, wenn sie sagen sollen, was „um eins mehr als fünf“ ist bzw. „um wie viel mehr fünf als sechs“ ist: Ihr Zahldenken bietet offenbar noch keine ausreichende Grundlage für Zahlvergleiche.

Sinnvolle Maßnahmen zur Erarbeitung der Begriffe „mehr“, „weniger“, „gleich viel“

• Anzahl-Vergleiche ohne Zählen bei inhaltlich einander zugeordneten Dingen anregen und besprechen: Sind im Klassenzimmer mehr Stühle oder mehr Kinder? Muss man zählen, um das sagen zu können? Sind auf dem gedeckten Tisch mehr Löffel oder mehr Gabeln? Usw.
• Dabei Klärung der Begriffe „gleich viel“, „mehr“ und „weniger“ mit Bezug auf einen Eins-zu-Eins-Vergleich zweier Anzahlen: Es sind mehr Stühle, weil ein Stuhl in der Klasse unbesetzt ist (Franzi ist krank). Es sind gleich viele Löffel und Gabeln, weil bei jedem Löffel genau eine Gabel liegt, usw.
• Anwendung dieses „Vergleichs-Verfahrens“ auf beliebige Anzahl-Vergleiche. Dabei geht es natürlich nicht darum, das zählende Vergleichen zu „verbieten“ (welches ja bei größeren, nicht paarweise angeordneten Mengen in der Regel das ökonomischere Verfahren darstellt). Kinder sollten aber wissen, dass es „auch anders geht“, nämlich durch Zuordnen.
• Vertiefen des Verständnisses der Vergleichswörter durch Aktionen und Fragen wie:
  • Jetzt sind es gleich viele; was ist, wenn ich bei der einen Reihe eins weg nehme / bei der anderen Reihe eins dazu gebe?
  • Jetzt sind es gleich viele. Da nehme ich eines am Anfang weg, dort nehme ich eines in der Mitte weg. Wie ist es dann?
  • Jetzt ist da um eins weniger – was kann ich tun, damit es wieder gleich viele werden?
• Aus solchen Versuchen sollte das Verständnis für die „Erhaltung der Anzahl“ gewonnen werden: Eine Anzahl bleibt gleich viel, solange ich nichts dazu gebe oder wegnehme. Habe ich die Finger einer Hand abgezählt und als „fünf“ bestimmt, dann bleiben es fünf (solange kein böses Missgeschick passiert).
• Anzahl-Vergleiche auch durch vorstellendes Zuordnen bei entsprechend geordneten Mengen („Blick schulen“, „Zuordnen mit den Augen“) versuchen.
• Das zuordnende Vergleichen bewusst auch bei großen Anzahlen anwenden: Hier gibt es ja keine Beschränkung durch Zahlwortkenntnisse!
• Verknüpfen von Zählen und Zuordnen: Von zwei einander eins-zu-eins zugeordneten Reihen wird nur eine gezählt; anschließende Frage: Wie viele sind in der anderen?
• Einbezug von Situationen, in denen die räumliche Anordnung zu Fehlurteilen verleitet (siehe oben, „die dunklen roten Punkte sind mehr“). Worum es hierbei vor allem geht: Erkennen, dass man dem „Augenschein“ nicht ohne weiteres trauen kann – und (sei es durch Zählen oder Zuordnen) besser nachprüfen sollte.

Auffälligkeiten beim „ersten Rechnen“

• Nicht nur das Aufsagen der Zahlwortreihe, auch das Lösen von einfachen Additionen und Subtraktionen gelingt den meisten Kindern bereits im Kindergartenalter. In der Regel erfolgt es zählend, unter Zuhilfenahme von Fingern und Material (Würfel, Plättchen usw.).Viele Kinder entwickeln dabei weitgehend von selbst ein fortgeschritteneres Zählverfahren: Sie zählen etwa bei „vier und drei“ erst vier Würfel ab und legen dann mit den Worten „fünf, sechs, sieben“ noch drei Würfel dazu. Oder sie kontrollieren das Weiterzählen um drei Schritte mit den Fingern.
  Andere Kinder wenden noch ein weit umständlicheres Verfahren an: Sie zählen zunächst „eins, zwei, drei, vier“ Würfel ab, dann daneben „eins, zwei, drei“ andere Würfel und ermitteln schließlich die Gesamtanzahl, indem sie von eins weg alle Würfel noch einmal zählen.Dieses „Alles-Zählen“ (im Unterschied zum „fortgeschritteneren“ „Weiterzählen“) ist als Hinweis auf einen möglichen Entwicklungsrückstand im Zahlverständnis ernst zu nehmen. Umgekehrt sollte es im Unterricht freilich nicht darum gehen, dass diese Kinder nun Rechnungen durch Weiter- bzw. Zurückzählen lösen lernen – sondern gerade darum, dass alle Kinder Wege finden, Additionen und Subtraktionen gänzlich ohne Zählen zu lösen (siehe unten).

• Manche Kinder fallen dadurch auf, dass sie beim zählenden Lösen von Additionen und Subtraktionen im Ergebnis immer wieder um eins „daneben liegen“. Dies sollte nicht als „Verzählen“ oder „Schlampigkeit“ übergangen werden: Möglicherweise steckt System und Logik (im Sinne einer bestimmten Auffassung von Zahlen und Rechenoperationen) dahinter. „Vier und drei ist sechs“ kann beispielsweise so gedacht werden:
  “eins, zwei, drei, vier“ (dabei werden vier Finger ausgestreckt); „eins (dabei wird der vierte Finger angetippt), zwei (dabei der fünfte ausgestreckt), drei (dabei ein sechster ausgestreckt).“ So entsteht das „Fingerbild“ der Zahl sechs, die folgerichtig als Antwort gegeben wird.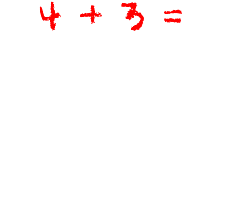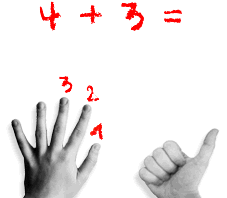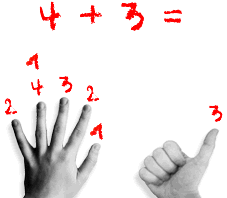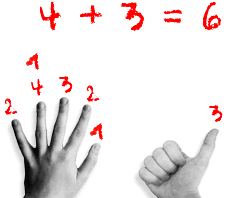

Auf diese Weise ist der „Fehler um 1“ keine „Schlamperei“, sondern konsequent im Sinne einer bestimmten Denkweise über Zahlen (die als „Stationen“ in einer Reihe, nicht als Anzahlen verstanden werden) und daher auch über das Addieren (das als „Weiterhüpfen“ in der Reihe, nicht als „Dazugeben“ oder „Zusammengeben“ gedacht wird).

Auch hier gilt: Die didaktische Antwort auf „Fehler um 1“ sollte sich nicht darin erschöpfen, dem Kind eine Zählstrategie zu zeigen, die zu richtigen Lösungen führt (etwa im obigen Beispiel: „Du musst bei fünf weiterzählen!“). Worum es vielmehr geht: Dass Kinder Zahlen und Rechenoperationen in einer Weise verstehen lernen, die es ihnen ermöglicht, Aufgaben im Zahlenraum bis zehn (und auf dieser Grundlage in beliebigen Zahlenräumen) ohne Zählen zu lösen.

Förderhinweise für das erste Rechnen finden Sie auf diesen Seiten unter Anschauungsmaterial im Zahlenraum 10 und sehr ausführlich im Buch Rechenschwäche vorbeugen.

Nicht nur für „Risikokinder“ wichtig: Gezieltes Hinarbeiten auf nicht-zählendes Rechnen!

Ende des ersten Schuljahres sollten Kinder die Grundaufgaben im Zahlenraum zehn weitgehend automatisiert haben (vgl. Schipper 2005).

Freilich: Das Loskommen von zählenden Lösungsverfahren ist keine „natürliche Entwicklung“, die früher oder später „von selbst“ (und bei manchen Kindern dann rätselhafter Weise scheinbar gar nie) eintritt. Rechnen im eigentlichen Sinne, also nicht-zählendes Lösen von Rechenaufgaben, ist (wenn es denn zustande kommt) immer eine Folge von Lernprozessen.

Diese Lernprozesse können wir Erwachsene unterstützen, aber auch durchaus erschweren – je nachdem, welche Art von Unterricht wir Kindern bieten, welche Förderung wir ihnen zuteil werden lassen. Das gilt grundsätzlich für „Risikokinder“ im Sinne dieses Artikels ebenso wie für „durchschnittliche“ oder gar „hochbegabte“ Kinder.

Um also – möglichst mit allen Kindern! – das (äußerst anspruchsvolle!) Ziel „nicht-zählendes Rechnen“ bis zum Ende des ersten Schuljahres zu erreichen, ist vom Beginn des ersten Schuljahres weg gezielte Unterrichtsarbeit notwendig. Hier geht es nicht mehr nur um „vorbeugende Arbeit mit Risikokindern“, sondern um zeitgemäßen Mathematikunterricht generell.

Wir hoffen, dass Sie auf diesen Seiten (siehe die weiteren „Fördertipps“) und in der „Weiterführenden Literatur“ (siehe unten) dafür hilfreiche Anregungen finden werden!