Tel. 01 / 526 48 46
Rechenschwache Kinder verstehen Zahlen zumeist nicht als Menge (Quantum, Anzahl). Sondern gewissermaßen als Punkt in einer Reihe, als eine Station in einer Kette von Zahlennamen. „Sieben“ beispielsweise wird nicht als Gesamtheit von sieben Einern aufgefasst, sondern als der siebente, das eine Ding (Würfel, Finger …), auf welches der Finger beim Aufsagen der Abzähl-Reihe zuletzt getippt hat.
Der Material-Einsatz muss also darauf abzielen, diese auf den Reihenfolge-Gedanken („Ordinal-Aspekt“) der Zahl eingeschränkte Sicht zu korrigieren. Das verlangt ein striktes Wegführen des Kindes vom rein zählenden hin zum Mengen erfassenden, Mengen vergleichenden und Mengen strukturierenden Zahlen-Umgang. Nun lässt sich aber so gut wie jedes Material auch rein zählend gebrauchen. Eben deshalb hängt gerade bei der Erarbeitung des richtigen Zahlverständnisses alles von der Art und Weise ab, wie das Material verwendet wird. Freilich gibt es auch dafür mehr oder weniger gut geeignete Materialien.
Die folgenden Überlegungen beziehen sich stets auf die – therapeutisch unerlässliche – Situation der Einzelarbeit mit einem Kind. Sie können keinesfalls eins zu eins auf die Klassenarbeit übertragen werden. In der Klassenarbeit spielen Gesichtspunkte wie leichte Handhabbarkeit, Möglichkeiten einer missbräuchlichen Verwendung durch das nicht individuell angeleitete Kind u.v.m. eine wesentliche Rolle – Gesichtspunkte, die in der Einzelarbeit nicht oder nur bedingt zu berücksichtigen sind.
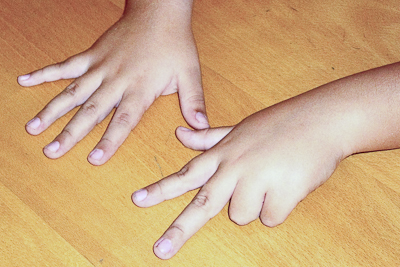Finger beim Rechnen – das ist mitunter tabu. Auch Lehrer, die vielleicht selbst eine unverkrampfte Haltung dazu einnehmen, müssen bedenken, dass viele Eltern, Großeltern, bei Hausübungen helfende Verwandte… ab einem gewissen Alter „Finger-Verbote“ aussprechen – in der irrigen Annahme, schon alleine dadurch dem Kind zum anschauungs-ungebundenen Kopfrechnen zu verhelfen.
Tatsache ist aber: Ein Kind mit einer wie oben beschrieben falschen Zahlvorstellung wird auch bei „einfachen“ Plus- und Minus-Aufgaben nur durch Zählen zu einer Lösung finden. Verbietet man ihm nun eine Zähl-Hilfe (Finger, Würfel, Knöpfe, Bleistifte …), dann führt das nur entweder zu Heimlichkeiten (Finger unter dem Tisch, unter dem Popo, nur leichtes „Finger-Drücken“ an der Wange …).
Oder aber dazu, dass das Kind nun tatsächlich ohne Zähl-Hilfe dennoch zu zählen versucht. Es wird dann – zumeist mit allen äußeren Zeichen größter Anspannung (Augen fest zugekniffen, den Kopf im Zähl-Takt mitbewegend…) – im Kopf die Zahlenreihe Schritt für Schritt rauf- oder runterhüpfen.
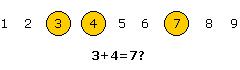Das ist eine gewaltige Anstrengung von Wille und Konzentration – aber mathematisch um nichts wertvoller als das ungleich leichtere und auch weniger fehleranfällige Abzählen an Fingern oder Würfeln oder sonstigen Zähl-Hilfen.Vom Standpunkt eines rein ordinalen Zahlverständnisses (Zahl als Station, nicht als Menge gedacht) könnte „3 + 4“ ebensogut „2“ ergeben – nämlich „2 Stationen“.
Das Problem bei jedwedem Zählen – ob mit oder ohne Finger – besteht darin, dass die Zahl nicht als Menge, nicht in ihrer Größe, ihrem „Wie viel?“ genommen wird. Aber das passiert eben deshalb, weil das rechenschwache Kind die Zahl bereits als nicht-mengenhaft versteht. Das Zählen ist also nur die Folge-Erscheinung des dahintersteckenden eigentlichen Problems namens „falsche Zahlvorstellung“.
Deshalb ist ein „Verbot“ des Zählens keine Lösung, im Gegenteil: es macht – siehe oben – die Situation für das Kind nur noch schlimmer.
Das dauerhafte Zählen-Dürfen hilft dem Kind allerdings auch nicht: Die Hoffnung, das Kind werde schon irgendwann von alleine auf das Zählen verzichten, erweist sich im Fall einer Rechenschwäche leider als illusorisch. Worum es vielmehr geht, ist dem Kind alternative, mengen-bezogene Weisen der Zahlverknüpfung zu eröffnen. Und gerade dafür sind, richtig verwendet, die Finger wiederum sehr brauchbar.
Nur dürfen sie dann eben nicht als bloße Abzähl-Hilfe, einen nach den anderen antippend oder ausstreckend, verwendet werden.
Sondern als Hilfe zur Erarbeitung einer Modell-Vorstellung für die Mengen-Gliederung der Zahlen bis 10.
Gemeint ist: Das Kind soll lernen, mit 5 die Vorstellung „alle Finger auf einer Hand“ spontan zu verknüpfen. Mit 10 „alle Finger auf beiden Händen zusammen.“ Mit z.B. 8 die Vorstellung „auf einer Hand 5, auf der anderen 3“. Und in weiterer Folge: Mit z.B: 6 die Vorstellung „4 Finger brauche ich dafür nicht; also 4 Finger noch dazu, dann sind’s alle 10“.
Diese Vorstellungen werden sich bei nicht-rechenschwachen Kindern in der Regel früher oder später wie von selbst einstellen. Für rechenschwache Kinder dagegen ist es oft noch in der 3. Schulstufe unmöglich, sich die Zahl 8 anders als durch Einzeln-Hochzählen der 8 Finger mühsam zu erarbeiten.
Das heißt aber nicht, dass dieses „innere Fingerbild“ für rechenschwache Kinder nicht erreichbar wäre; es heißt nur, dass man es gezielt und geduldig, Schritt für Schritt, mit ihnen erarbeiten muss.
Gefragt wäre also in einer ersten Phase die Erarbeitung einer inneren Vorstellung davon, wie die Zahlen bis 10 mit Fingern gezeigt werden können. Dies geschieht zunächst natürlich unter tatsächlichem Einsatz der Finger. Wichtig ist es aber, diesen tatsächlichen Gebrauch der Finger allmählich durch die innere Vorstellung zu ersetzen. Dafür muss das Kind immer wieder dazu angehalten werden, das, was sich durch Hochzählen einer Zahl an den Fingern ergibt, in Worte zu fassen:
„Ich habe jetzt 8 Finger ausgestreckt, auf einer Hand 5, auf der anderen 3 Finger.“
Ein möglicher weiterer Zwischenschritt: Das Kind soll die Zahl mit den Fingern zeigen – aber unter dem Tisch oder unter einem Tuch. Es kann die Finger also spüren, aber nicht sehen – und soll nun dennoch versuchen zu sagen, wieviele Finger es jetzt an beiden Händen ausgestreckt hält bzw. wieviele Finger nicht ausgestreckt sind. Von diesem „inneren Finger-Bild“ der Zahl ausgehend lassen sich eine Fülle mathematischer Operationen unschwer erarbeiten:
Wenn 8 immer auch als „5 + 3“ gedacht wird, ist 5 + 3 = 8 ebenso unschwer zu erarbeiten (und später vom Kind dauerhaft zu merken) wie 8 – 5 = 3 oder 8 – 3 = 5 und vieles andere mehr.
Immer freilich gilt: Die Finger werden nicht einzeln abzählend eingesetzt, sondern in „Hand-Paketen“, das heißt als Gliederungshilfe für die Zahlen mit den Bezugspunkten 5 (=eine ganze Hand) und 10 (=beide Hände zusammen).
Das „innere Fingerbild“ muss in einem nächsten Schritt erweitert werden: 8 soll nicht nur mit „5 + 3“ assoziiert werden, sondern ebenso problemlos mit „4 + 4“, „6 + 2“, „1 + 7“ etc.
Dazu bedarf es der zusätzlichen Einsicht, dass ich einen Einer-Haufen beliebig in zwei kleinere Einer-Haufen zerteilen kann – und diese Verteilung durch Verschieben einzelner Einer beliebig variieren kann, ohne an der Gesamt-Anzahl der Einer etwas zu ändern.
Auch dafür lassen sich die Finger sinnvoll nutzen – indem das Kind aufgefordert wird, 7 mit anderen als den gewohnten Fingern zu zeigen, also z.B. ohne den Daumen der rechten Hand.
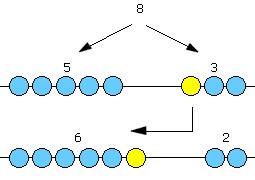Leichter nachvollziehbar ist das Prinzip „hier eins mehr, dort eins weniger, insgesamt gleich viel wie zuvor“ jedoch an der Kugelkette. Dafür 3, 4, 5, … bis 9 Holzkugeln auf je einer Schnur auffädeln. Daran mit dem Kind zunächst den oben beschriebenen Grundgedanken erarbeiten. Das Kind in der Folge verschiedene Zerlegungen einer Zahl selbst an der Kugelkette durchführen und jeweils notieren lassen. Im nächsten Schritt wieder der Versuch, das Material durch Vorstellung zu ersetzen:
Ausgangspunkt ist z.B. die „Handzerlegung“ der 8 in 5 + 3. Diese wird an der 8er-Kette gelegt. Dann die Kette mit Tuch verdeckt, Kind verschiebt unter dem Tuch eine Kugel von der 3er-Seite zur 5er-Seite – und soll nun (ohne unter dem Tuch zu zählen!) versuchen, die entstandene neue Zerlegung/Verteilung der 8 Kugeln anzugeben.
Wieder wird ein Kind mit Defiziten in der Verinnerlichung hier wahrscheinlich Probleme haben. Dann aber nicht einfach die Kette wieder aufdecken, sondern konkrete Denk-Anstöße geben: „Überlege zunächst nur, was auf dieser Seite passiert ist.“ „Hast du hier eine Kugel dazu geschoben?“ „Oder von hier eine Kugel weggeschoben?“ „Ist es hier mehr als vorher oder weniger als vorher?“
Die pädagogische Kunst besteht wieder darin, so wenig von diesen Anregungen wie möglich, so viele wie nötig zu geben.
Für das Erarbeiten eines Grundverständnisses mathematischer Operationen (Addieren als Dazugeben, Zusammenfügen, Subtrahieren als Wegnehmen, Unterschieds-Bestimmen…), das Anstellen von Mengenvergleichen und vieles mehr ist das Handeln mit konkretem Material unerlässliche Voraussetzung.
Wegen ihrer vielfältigen Einsatzmöglichkeiten auch für weitere Schritte (etwa beim Ein-mal-Eins) haben sich dafür Steck-Würfel sehr bewährt: Sie erlauben farbliche Differenzierung, die Möglichkeit des Zusammen- und wieder Auseinandersteckens läßt sich vielfach verständnisfördernd einsetzen, sie sind Kindern wegen ihrer Eignung zum Basteln in der Regel sympathischer als simple Klötzchen, Knöpfe, Plättchen.
Ein Nachteil besteht sicherlich in der schweren Handhabbarkeit für Kinder mit Defiziten in der Feinmotorik; man kann hier nur an die Produzenten appellieren, leichter steckbare, zudem auch etwas größere als die erhältlichen (Kantenlänge ca. 1,5 cm) herzustellen.
Wesentlich ist wieder die Verwendung der Würfel: Als bloße Zählhilfe benutzt, taugen sie in keinster Weise zum Aufbau tragfähiger innerer Vorstellungen.
Insofern stimmt die Kritik, die Lorenz/Radatz im schon zitierten „Handbuch des Förderns im Mathematikunterricht“ an den Steckwürfeln anbringen. Nur: Als Zählhilfe „missbrauchen“ lässt sich so gut wie jedes Material. Nicht die Steckwürfel sind also das Problem, sondern ein falscher Umgang damit.
Falsch wäre etwa die Hoffnung, dass das Kind eine bestimmte Anzahl wie etwa 7 nur oft genug mit Würfeln hinlegen und anschauen müsste, um die Zahl als Menge zu erfassen und dann auch anschauungsungebunden mit ihr operieren zu können. Warum das in der Regel nicht funktioniert, ist oben erklärt: Das Kind nimmt die Würfel (vielleicht) dankbar als Zählhilfe. Es „sieht“ aber die Menge nicht, weil es aufgrund seiner bereits fehlerhaften Zahlauffassung darauf gar nicht achtet.
Deshalb muss auch bei der Arbeit mit Steckwürfeln von der Betreuungsperson aktiv darauf abgezielt werde, dass das Kind einen Mengen vergleichenden, nicht-zählenden Standpunkt zum Material einnimmt.
Ein Beispiel dafür: Das Kind weiß 3 + 3 auswendig, 3 + 4 muss stets durch Abzählen gelöst werden.
Hier empfiehlt es sich, beide Aufgaben mit Steck-Würfeln legen zu lassen – aber gerade nicht nach dem „Wieviel?“ zu fragen, sondern: „Vergleiche die Aufgaben. Wo sind insgesamt mehr Würfel?“
Die Frage befreit vom Druck, immer gleich ein „Ergebnis“ wissen zu müssen und lädt zum Nachdenken ein: Auf beiden Seiten sind zuerst 3, dann kommen hier 3 dazu, da aber 4, also mehr – dann müssen es auch insgesamt mehr sein.
Dieses Nachdenken wird wieder dadurch gefördert (und der Reflex des Sofort-Abzählen-Wollens gezähmt), dass die gesamte Würfel-Anordnung unter einem Tuch verschwindet. Die Erinnerung an die Handlung bleibt und kann von der Betreuungsperson durch gezielte Fragen strukturiert werden.
In ähnlicher Weise lassen sich sämtliche Grundaufgaben im Zahlenraum 10 erarbeiten. Damit diese auch einem rechenschwachen Kind letztlich anschauungs-ungebunden gelingen, bedarf es freilich eines in kleinste Schritte unterteilten systematischen Neu-Aufbaus unter Berücksichtigung der individuellen Ausgangslage.
Dazu ist oben im Grunde alles Nötige gesagt. Das Wichtigste noch einmal: Ein Verbot des Finger-Abzählens ist nicht zielführend. Es geht darum, mit dem Kind in der oben angedeuteten Weise Alternativen zum Abzählen zu erarbeiten. Wenn das Finger-Zählen bereits zur Gewohnheit geworden ist, ist zu seiner Überwindung freilich oft ein hohes Maß an psychologischem und pädagogischem Fingerspitzengefühl erforderlich.
Sofern nur einzelne 1-Euro-Stücke als konkretes Material (wie Würfel, Knöpfe…) verwendet wird, gelten alle Vorbehalte, die oben beschrieben wurden: Das Anschauen und Hin- und Herschieben bewirkt von sich aus noch keine Einsicht, eher besteht die Gefahr, dass die 1-Euro-Stücke bloß als Zähl-Hilfe gebraucht werden.
Noch problematischer ist in dieser Phase die Verwendung von unterschiedlichen Einheiten (10-€-Scheine, 5-€-Scheine, 2-€Stücke, 1-€-Stücke, eventuell auch noch Cent). Zu verstehen, dass z.B. ein Fünfer mehr ist als 4 Einer, setzt bereits einiges an richtigem Zahl-Verständnis voraus. Das Hantieren mit Fünfern und Einern eignet sich also wenig zum Erwerb dieses grundlegenden Verständnisses.
Der scheinbar so einfach zu verstehende Zahlenstrahl wirft – speziell für rechenschwache Kinder – eine Fülle von Fragen auf. Warum steht die „1“ unter dem 2. Sticherl? Warum ist die „0“ auch ein Stricherl, wo „null“ doch „nix“ heißt? Warum soll von 3 auf 7 noch vier fehlen, wo doch zwischen dem dritten und dem siebenten Stricherl nur drei Stricherl liegen?
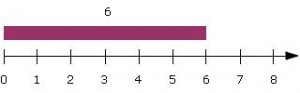Diese Verwirrungen sind wieder Ausdruck der falschen Zahlvorstellung des rechenschwachen Kindes: Die Zahl, jetzt am Zahlenstrahl dargestellt, wird als Position genommen – also als das eine Stricherl, unter welchem die jeweilige Ziffer steht.
Der Zahlenstrahl scheint freilich diese Auffassung der Zahlen sogar zu bestätigen: Was soll denn 6, am Zahlenstrahl betrachtet, denn sonst sein, wenn nicht die mit „6“ bezeichnete Markierung?
Tatsächlich empfehlen manche Schulbücher, genau diese („ordinale“) Deutung der 6 am Zahlenstrahl auch mit den Kindern im Erstunterricht zu erarbeiten. Davor möchten wir an dieser Stelle aus der Perspektive von Rechenschwäche-Therapeuten eindringlich warnen. Auf diese Weise werden Missverständnisse, sofern bereits vorhanden, verstärkt, sofern noch nicht vorhanden, möglicherweise sogar erst provoziert.
Wenn schon der Zahlenstrahl im Erstunterricht Verwendung finden soll, dann müsste er sorgfältig als Maßzahl-Darstellung erarbeitet werden: 6 ist eben auch am Zahlenstrahl nicht ein Ding, ein „Stricherl“. Sondern die Gesamtheit von 6 Einheits-Strecken, wobei eine Einheits-Strecke jeweils der Abstand zwischen zwei Markierungen ist.
Zahlen müssen am Zahlenstrahl also als Strecken verstanden werden. So erarbeitet, unterstützt der Zahlenstrahl einerseits ein quantitatives Zahlverständnis. Andererseits wird erst so der Zahlenstrahl selbst handhabbar, werden die oben angeführten Probleme am Zahlenstrahl selbst lösbar.
Es stellt sich allerdings die Frage, ob es – angesichts der Fülle möglicher Missverständnisse – wirklich sinnvoll ist, den Zahlenstrahl überhaupt im Erstunterricht einzusetzen. Wir empfehlen generell einen späteren Einsatz – zum Aufbau einer Zahlenraumvorstellung im Hunderterbereich (siehe dort). Die Notwendigkeit, den Zahlenstrahl zunächst als „Längen-Modell“ der Zahl zu erarbeiten, besteht natürlich aber bei späterer Verwendung.