Der „Gipfel des Grauens“ – und wie er seinen Schrecken verliert: Einige Anregungen für die gezielte Förderung bei Textaufgaben
Autoren: Michael Gaidoschik und Eva Lassnitzer
1. Warum Textaufgaben (nicht nur, aber besonders auch) für „rechenschwache“ Kinder so schwierig sind
„Mein Kind kann nicht logisch denken!“ – Das ist ein Satz, den wir in unserem Institut immer wieder zu hören bekommen. Und als Begründung für dieses harte Urteil wird zumeist die Art und Weise angeführt, wie das betroffene Kind mit dem wohl für alle Kinder schwierigsten Bereich der Grundschulmathematik umgeht: Textaufgaben.
Dazu ein beliebiges Beispiel:
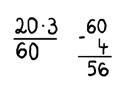 Ein 10jähriges Mädchen wird von uns Ende der vierten Schulstufe mit folgender Aufgabe konfrontiert: „Ein Tischler zersägt ein 3m20 langes Brett in 4 gleich lange Stücke. Wie lange ist jedes Stück?“ Das Mädchen fängt sofort zu rechnen an. Die Antwort: „Jedes Stück ist 56 Meter lang!“
Ein 10jähriges Mädchen wird von uns Ende der vierten Schulstufe mit folgender Aufgabe konfrontiert: „Ein Tischler zersägt ein 3m20 langes Brett in 4 gleich lange Stücke. Wie lange ist jedes Stück?“ Das Mädchen fängt sofort zu rechnen an. Die Antwort: „Jedes Stück ist 56 Meter lang!“
Mangel an Denkfähigkeit? Das scheint angesichts solcher Hervorbringungen eine plausible Erklärung zu sein. Andererseits: Dieselben Eltern, die hier „Logikmangel“ vermuten, kennen ihr Kind und wissen genau, wie aufgeweckt es in anderen Zusammenhängen oft ist.
Und bei allen unbestreitbaren Unterschieden in dem, was man in der Psychologie als „Intelligenz“ bezeichnet:
Ein Kind, das sich etwas logisch so Anspruchsvolles wie Sprache angeeignet hat; das sich in seiner komplexen Umwelt zurechtfindet; ein Kind, das auch in der Schule (bei allen vielleicht vorhandenen Problemen) bestimmt schon vieles gelernt hat – so ein Kind stellt doch Tag für Tag unter Beweis, dass es grundsätzlich sehr wohl in der Lage ist, logische Zusammenhänge zu erkennen und Schlussfolgerungen zu ziehen.
Wie sind aber dann so „kopflose“ Bearbeitungen von Textaufgaben wie die oben geschilderte zu verstehen? Einen Teil der Erklärung liefern meines Erachtens die Untersuchungen von Mathematik-Didaktikern über den Umgang von Kindern mit sogenannten „Kapitänsaufgaben“; das namengebende, klassische Beispiel dazu:
„Auf einem Schiff befinden sich 26 Schafe und 10 Ziegen. Wie alt ist der Kapitän?“
Was tun nun Volksschüler, wenn man sie (ohne Vorwarnung!) mit solchen „Aufgaben“ konfrontiert; mit Texten also, die keine sinnvolle Rechnung zulassen?
Das hängt offenbar ganz davon ab, wie lange sie schon unterrichtet wurden: Eine Untersuchung an 333 (völlig „normalen“) Kindern von der Vorschule bis zur fünften Schulstufe (Radatz, 1983) ergab jedenfalls, dass dergleichen „Unsinnsaufgaben“ von ca. 10% der Erstklassler, ca. 30% der Zweitklassler und ca. 60% der Dritt- und Viertklassler „gelöst“ wurden.
Noch einmal: Diese Untersuchungen wurden mit völlig durchschnittlichen Volksschülern gemacht. Soll man jetzt also den Schluss ziehen, dass nicht nur rechenschwache Kinder, sondern generell etwa Viertklässler in ihrer Mehrzahl „nicht logisch denken“ können?
Gewiss nicht. Schon das Häufigerwerden der scheinbaren „Kopflosigkeit“ von Klasse zu Klasse zeigt ja, dass hier etwas ganz anderes als „Logikmangel“ eine gewichtige Rolle spielt: Offenbar lernen Kinder im Laufe der Jahre einen bestimmten Umgang mit Mathematik im Allgemeinen, Textaufgaben im Besonderen. Ein wesentlicher Grundsatz dieses Umgangs scheint zu lauten: „Wenn Zahlen dastehen, muss ich rechnen!“ Die (kritische) Auseinandersetzung mit dem Text gehört dagegen nicht zu diesem gelernten Verhalten. Aber das gilt eben keineswegs nur für rechenschwache Kinder!
Hier lässt sich also einerseits eine Gefahr erkennen, die der Mathematikunterricht für alle Kinder in sich trägt – und die natürlich nach „präventiven“ Maßnahmen verlangt (etwa dem gezielten Einsatz von „Kapitänsaufgaben“ im Unterricht, wie er in manchen Schulbüchern auch bereits vorgesehen ist).
Andererseits kann man leicht erklären, warum gerade „rechenschwache“ Kinder (ohne deshalb „dümmer“ zu sein als andere) dieser Gefahr des scheinbar beliebigen „Zahlenverwurstens“ besonders häufig erliegen:
- „Rechenschwäche“ bedeutet in der Regel: ein unzureichendes Zahlverständnis. Zahlen werden nicht (oder nicht vorrangig) als Anzahlen, nicht als „Wie viel?“ gedacht, sondern als „Stationen“ einer „Zahlenkette“. „69“ ist nicht als „sechs Zehner und noch 9 Einer“ im Bewusstsein, sondern etwa als „die 69. Kugel in der Kugelkette“.
- Auf dieser Grundlage können aber auch die Rechenarten nicht als das verstanden werden, was sie sind. Es handelt sich dabei ja nur um verschiedene Arten, mit Anzahlen umzugehen (Dazu- oder Zusammengeben, Wegnehmen, Vervielfachen, Aufteilen …). Ein „rechenschwaches“ Kind hat mir dagegen das „Dividieren“ einmal so erklärt: „Das ist das mit dem Doppelpunkt. Da muss ich das hinschreiben, was bei Mal vorne steht.“ Wie sollte dieses Kind auf Grundlage eines solchen „Operationsverständnisses“ erkennen, ob eine Textaufgabe nun so eine „Doppelpunktrechnung“ verlangt?
- Das Problem dieser Kinder beginnt also nicht erst bei der „logischen Herausforderung“, die vier Grundrechenarten in verschiedenen Sachsituationen „wieder zu erkennen“. Sondern sie haben bereits die vier Grundrechenarten nicht als das verstanden, was sie sind. Daher ist ein Wiedererkennen gar nicht möglich – zumindest nicht nach inhaltlichen Kriterien. Es ist, wie wenn man eine Rätselfrage gestellt bekommt – aber in einer Sprache, die man nicht versteht. Egal, wie schlau man ist: In so einer Situation ist man chancenlos.
- Wenn man aber einerseits chancenlos ist, andererseits der Aufgabe nicht entkommt – was tut man dann? Da gibt es zweifelsohne verschiedene Möglichkeiten; wir finden sie alle (oft in Mischformen) bei rechenschwachen Kindern vor:
Variante A: Verweigerung! – „Textaufgaben kann ich nicht/mag ich nicht.“
Variante B: Kamikaze! Drauflos! Augen zu und durch! – „Ich hab’ zwar keine Ahnung, wie das gehen soll, aber ein Ergebnis muss her, also probiere ich halt irgendwas.“
Variante C: Mehr und mehr verzweifeltes Bemühen, die Sache doch irgendwie in den Griff zu bekommen.
– Etwa dadurch, dass das Zahlenmaterial auf ganz und gar nicht unintelligente Weise nach Kriterien der Wahrscheinlichkeit „abgeklopft“ wird: „Zwei dreistellige Zahlen – das muss entweder plus oder minus sein!“ – schließlich wird in der dritten Klasse ja nur mit einstelligem Faktor multipliziert bzw. dividiert!
– Oder auch so: „Das ist sicher mal, weil vorher haben wir ja auch mal gerechnet!“
– Schließlich und vor allem aber dadurch, dass das Kind versucht, sich bestimmte Aufgabentypen im Sinne eines „Schemas“ zu merken: „Das ist eine mit Minuten. Da muss man immer mal 60!“ (Die Aufgabe hieß: „Peter kommt um 13. 58 Uhr zur Busstation. Der Bus fährt um 14.12 Uhr ab. Wie viele Minuten muss Peter warten?“)
Gerade Variante c) kann sogar eine Zeitlang immer wieder zum Erfolg führen – vor allem dann, wenn die von der Schule geforderten Textaufgaben entsprechend „berechenbar“ und „schematisch“ sind. Eine Kompetenz im „mathematischen Problemlösen“ kommt so freilich nicht zustande.
Was für alle drei Varianten (und die unzähligen Mischformen) gilt: Für rechenschwache Kinder sind Textaufgaben der „Gipfel des Grauens“ – „die, die ich immer nicht kann“. Und daher entsprechend beliebt…
2. Zum Verhältnis von „Vorbeugen“ und „Heilen“
Die Möglichkeiten, ein bereits „gestörtes“ Verhältnis zu Textaufgaben aufzuarbeiten, unterscheiden sich in mathematik-didaktischer Hinsicht nicht grundsätzlich von den Maßnahmen, die geeignet sind, um Kindern von Anfang an das Rüstzeug für die Lösung von Sach- und Textaufgaben zu vermitteln. Die Anregungen, die im Folgenden mit Blick auf den Erstunterricht („präventiv“) gegeben werden, sind also in gleicher Weise für die nachträgliche Aufarbeitung von bereits vorhandenen Schwierigkeiten geeignet.
Ein wesentlicher Unterschied besteht freilich: Bei Kindern, die bereits Misserfolgserlebnisse gesammelt haben, wird es oft besonderer pädagogischer und psychologischer Kunst bedürfen, um sie dazu zu bewegen, sich auf das vielleicht bereits verhasste Thema überhaupt noch einmal einzulassen. Vor allem gelernte „Schematiker“) klammern sich oft ängstlich an ihren (manchmal ja tatsächlich erfolgreichen!) „Lösungsweg“. In solchen Fällen ist es dann oft nicht damit getan, mit dem Kind und „am Kind“ zu arbeiten. Ein konkretes Beispiel: Ein Kind, das erst lernen muss, sich gedanklich auf einen Text einzulassen, wird das kaum schaffen, wenn es weiß: Nächste Woche ist Schularbeit, da gibt es dann wieder vier Textaufgaben (und sonst nichts!), bei denen ich (wenn überhaupt) nur dann eine Chance habe, wenn ich mir das dazu passende Rechenschema (ohne es zu verstehen) auswendig merke.
In solchen Fällen ist daher parallel zur Einzelförderung ein differenzierter Unterricht gefordert – und freilich auch ein radikales Umdenken bei jenen LehrerInnen und Eltern, die es bislang vielleicht sogar für sinnvoll gehalten haben, mit dem Kind unverstandene Rechenschemata „einzuüben“…
Selbstverständlich gilt aber auch hier: Vorbeugen ist besser als heilen. Eben deshalb wird im Folgenden – in der hier unvermeidlichen Kürze– ein „Aufbaukurs Textrechnen“ skizziert; ein Aufbaukurs, der in den ersten Monaten der ersten Schulstufe beginnen sollte. Je nach Defizitbereich sind aber, wie gesagt, die skizzierten Maßnahmen ebenso für die begleitende oder auch nachträgliche Förderung im Einzel- und Förderunterricht geeignet.
3. „Textrechnen“: Ein „Aufbaukurs“ in Stichworten
3.0. Vorbemerkung
Worauf hier aus Platzgründen nicht eingegangen werden kann, ist der Unterschied zwischen „Sach-“ und „Textaufgaben“. Selbstverständlich aber sind wir (wie wohl alle Fachdidaktiker) der Überzeugung, dass Sachrechnen nicht auf Textrechnen reduziert werden sollte; dass Sach- wie Textaufgaben einen Bezug zur Lebenswelt der Kinder haben sollten; dass es darum gehen sollte, den Kindern mit den Mitteln der Mathematik Wege zum Lösen realer Probleme zu erschließen – und nicht um das „Einkleiden“ von Rechenoperationen in weltfremde Fragestellungen (beliebiges Beispiel: „37 Anoraks kosten 1813 €. Wie viel kosten 24 Anoraks?“ – Bekanntlich ist in Geschäften ja immer der Preis von 37 Anoraks angeschrieben, obwohl man selbst nur 24 davon kaufen möchte …)
3. 1. Absichern des Operationsverständnisses der vier Grundrechenarten in allen Aspekten
Grundvoraussetzung dafür, dass ein Kind Textaufgaben verstehen kann, ist ein Operationsverständnis der vier Grundrechenarten in allen ihren Aspekten. Operationsverständnis erlangen Kinder aber nur durch eigene Handlungen mit geeignet strukturiertem Material.
Dazu noch einige nähere Ausführungen:
- Gerade auch dann, wenn eine Operation bereits automatisiert wurde, sollten „Rückübersetzungen“ in die jeweils zu Grunde liegende Material-Handlung immer wieder Thema im Unterricht sein (z.B. „12 : 4“ mit Würfeln durchführen lassen).
- Besondere Sorgfalt ist erfahrungsgemäß geboten bei folgenden Rechenarten bzw. Teilaspekten von Rechenarten:
– Minus nicht nur als Wegnehmen, sondern auch zur Ermittlung eines „Unterschiedes“
– Der gesamte multiplikative Bereich, und dabei noch einmal besonders das „Enthaltensein“ als ein Aspekt des Dividierens.
3. 2. Umsetzung in einschrittigen Sachaufgaben von Anfang an
Sach- (und dann Text-) Aufgaben sollten von den ersten Wochen an Thema das Mathematikunterrichts sein: Die auf jeder Stufe neu erworbenen Fähigkeiten im Umgang mit Zahlen befähigen schließlich jeweils auch zur Lösung von zuvor nicht lösbaren Fragestellungen des täglichen Lebens; ihr Einsatz dafür will aber auch noch gelernt werden!
Minimalanforderung ist dabei die Fähigkeit, mathematische Probleme zu lösen, die genau einen Rechenschritt verlangen.
Was zur Förderung dieser Fähigkeit beachtet werden sollte:
- Vermeidung von „Schema-F-Denken“ – und zwar von Anfang an. Das verlangt bei Sachaufgabestellungen von Anfang an die konsequente „Durchmischung“, etwa von Plus- und Malaufgaben (sobald beide Operationen jeweils für sich erarbeitet wurden) – anstelle des in Schulbüchern häufigen „Wir haben das schriftliche Multiplizieren gelernt, jetzt kommen dazu die Textaufgaben!“
- Kinder sollten immer wieder angeregt werden, (zunächst eben einschrittige) Sachaufgaben selbst zu erfinden; also Beispiele dafür zu finden, wo „im wirklichen Leben“ eine bestimmte Art des Rechnens notwendig ist.
- Das Schwierigste auf dieser Stufe, aber unumgänglich für die nächste Stufe (zweischrittige Aufgaben): Verschiedenes ist bekannt, was könnte man daraus berechnen? („Frage finden lassen“ zu einem „offenen Text“) Ein Kind, das nicht in der Lage ist, solche Fragen selbst zu formulieren, wird bei zwei- oder mehrschrittig zu lösenden Textaufgaben zwangsläufig anstehen.
3. 3. Text-Kompetenz als eigene Fertigkeit trainieren
Sofern Sachaufgaben als Textaufgaben präsentiert werden, muss eben auch der mathematisch orientierte, analytische Umgang mit Texten Inhalt gezielter „Trainingseinheiten“ sein.
- Unerlässliche „Spielregel“ für diese Einheiten: „Nichts ausrechnen!“ Es werden Texte untersucht – aber es geht gerade nicht darum, sofort die „passende Rechenart“ zu finden.
- Gerade auch um die Bereitschaft für einen solchen, „nicht auf die Lösung fixierten“ Umgang mit Texten zu wecken, empfiehlt sich der gezielte Einsatz von „Kapitänsaufgaben“.
Sinnvolle Übungen zur Steigerung der Textkompetenz
- Überflüssige Informationen aussieben lassen.
- Einen Text in eigenen (!) Worten nacherzählen lassen.
- Einen Text nachspielen lassen bzw. gemeinsam nachspielen; dabei „große“ Zahlen durch „kleine“ ersetzen (dadurch lässt sich auch eine Aufgabe ihrer mathematischen Struktur nach nachspielen, in der z.B. 258 Eier in Eierschachteln verpackt werden …)
- Die Text-Situation zeichnen lassen. Dabei ist zu beachten, dass nicht jedem Text mit einer Skizze beizukommen ist, und dass das Anfertigen einer mathematisch sinnvollen Skizze eine Fertigkeit ist, die erst an – dafür geeigneten Texten – gelernt werden muss!
- Den Text lesen lassen, dann abdecken und gezielte Fragen zum Text beantworten lassen.
- Mehrere Fragen zu einem Text anbieten – welche Frage ist sinnvoll?
- Mehrere Antworten zu einem Text anbieten – welche davon ist sinnvoll?
3.4. Systematische Erarbeitung der Lösungs-Kompetenz
Das Erfassen des Textes ist zwar die unverzichtbare Voraussetzung dafür, das darin formulierte mathematische Problem zu „knacken“. Aber das „Knacken“ selbst will natürlich auch gelernt sein. Und es wird wohl so sein, dass diese „Fähigkeit zum Problemlösen“ auch bei bestem Unterricht nicht bei allen Kindern im selben Maße heranreifen wird. Doch was alle Kinder mit Sicherheit lernen können, sind Strategien im selbständigen Umgang mit mathematischen Problemstellungen – Strategien, die jedenfalls die Chance erhöhen, dass der kindliche Geist auch in der Bearbeitung von Textaufgaben wirklich das leistet, was er eben individuell zu leisten imstande ist.
Die Vermittlung solcher Strategien (und nicht das Einüben von bestimmten Aufgabentypen) sollte daher in weiterer Folge im Zentrum des Sachrechenunterrichtes stehen.
Auch dafür einige Anregungen in Stichworten:
- Die Schwierigkeit einer Textaufgabe hängt nicht nur, aber auch davon ab, ob das Problem in einem, zwei oder mehreren Schritten gelöst werden kann. Diese Schwierigkeitsstufen sollten also auch bei der Erarbeitung der Problemlösungskompetenz beachtet werden.
- Wie bereits angedeutet: Zweischrittige Aufgaben können nur gelöst werden, wenn (vor der eigentlichen, im Text gestellten Frage) eine Zwischenfrage beantwortet wird. Diese Zwischenfrage kann anfangs vorgegeben werden. In weiterer Folge ist aber gerade darauf hinzuarbeiten, dass Kinder die im Text enthaltenen Informationen daraufhin untersuchen, welche Fragen damit unmittelbar beantwortet werden können.
- Dabei hilft es, wenn die Texte anfangs im Layout nach Sinneinheiten gegliedert werden, d.h.: Je Zeile oder Absatz ist nur jeweils eine mathematisch verwertbare Information enthalten. Die Kinder lesen jeweils einen Absatz (der Rest des Textes wird eventuell zugedeckt) und überlegen: Lässt sich damit etwas ausrechnen? Was lässt sich ausrechnen?
- Übersichtliches Aufschreiben ist als Kunst für sich zu trainieren.
- Nach jedem Schritt sollte nicht bloß eine Zahl als Ergebnis festgehalten werden, sondern überlegt und in Kurzform aufgeschrieben werden, was da jetzt jetzt eigentlich ausgerechnet wurde („Zwischenantwort“).
- Bei mehrschrittigen Aufgaben sollten die Kinder sich eine „Vollständigkeits-Überprüfung“ zur Gewohnheit machen: „Habe ich mit dem letzten Rechenschritt auch wirklich das ausgerechnet, was ich wissen wollte?“
Bei all dem gilt
Die Lehrerin/Förderperson sollte sich vor „Erklärungen“ oder gar „Anleitungen“ („Da musst du zuerst plus, dann mal rechnen!“) hüten:
- Wenn ein Kind den Text versteht
- wenn es ein umfassendes Verständnis der Rechenoperationen mitbringt
- wenn es darüber hinaus über Strategien der Problemlösung verfügt
- wenn schließlich die Problemstellung der Lebenswelt des Kindes angemessen ist –
dann sollte die Lösung des Problems letzlich vom Kind selbst gefunden werden können. Was es allenfalls noch braucht, sind Anregungen, in die eine oder andere Richtung zu überlegen – und vielleicht jemanden, der ihm Mut zuspricht, die Aufgabe auch alleine schaffen zu können.
Dieser Mut wächst freilich mit jeder selbständig gelösten Aufgabe!
Weiterführende Literatur
Abele, A./Kalmbach, H. u.a.: Handbuch zur Grundschulmathematik, Band 2, drittes und viertes Schuljahr. Klett-Verlag 1994.
Schipper, W./Dröge, R/Ebeling, A.: Handbuch für den Mathematikunterricht, 4. Schuljahr. Schroedel-Verlag 2000.
Spiegel, H./Selter, Ch.: Kinder & Mathematik. Was Erwachsene wissen sollten. Kallmeyersche Verlagsbuchhandlung 2003.