Größen: Messen – Schätzen – Umwandeln
Sicherheit durch Begreifen – Anregungen für einen verständnisorientierten Unterricht
Autoren: Eva Lassnitzer und Michael Gaidoschik
Autoren: Eva Lassnitzer und Michael Gaidoschik
Der Umgang mit Größen wird von Lehrkräften häufig als Schwachstelle von Schüler*innen genannt: mangelnde Größenvorstellung, absurde Schätzangaben und Ratlosigkeit beim Umwandeln von Maßeinheiten sind bekannte und oft attestierte Schwierigkeiten.
Das Umwandeln stellt mit Sicherheit einen der großen Stolpersteine der Grundschulmathematik dar. Viele Schüler*innen, bei weitem nicht nur die sogenannten „rechenschwachen“, bewältigen Umwandelaufgaben nur mithilfe mitgelieferter Tabellen inklusive vorgegebener Bedienungsanleitungen, häufig aber ohne jedes Verständnis. Sie sind daher hilflos, wenn keine „Ausfüllhilfen“ und „Anleitungen“ zur Verfügung stehen.
Ohne vorgegebenes Schema wird Umwandeln gerne auch als eine Art Glücksspiel betrieben. Dieses existiert in zwei Fassungen, je nach bereits erarbeitetem Zahlenraum: bis zur vierten Schulstufe heißt es „Nullen anhängen oder streichen“, später wird daraus „Komma verschieben“.
Beiden Zugängen gemeinsam ist das Prinzip der weitgehenden Zufälligkeit: Ob und wie viele Nullen angehängt oder gestrichen werden; ob, um wie viele Stellen und in welche Richtung das Komma verschoben wird, das muss aufgrund mangelnden Verständnisses zwangsläufig willkürlich entschieden werden. Wird Umwandeln aber als unverstandenes Regelwerk betrieben, ist und bleibt die Fehlerquote hoch, und das oft bis weit über die Schulzeit hinaus.
Schematische Übungsformate sind vermutlich gut gemeint, aber geradezu kontraproduktiv, wenn es um einen verständigen Umgang mit solchen Aufgaben geht. Wenn ganze Aufgabenblöcke das Umwandeln in jeweils eine Richtung erfordern, z.B. mit Formulierungen wie: „Wandle (folgende 30 Aufgaben) in die nächstkleinere Einheit um“, und dann getrennt davon umgekehrt: „Wandle (folgende 30 Aufgaben) in die nächstgrößere Einheit um“ trägt das ganz wesentlich dazu bei, dass Schüler*innen auf die Idee kommen, den Zahlen zu entnehmen, ob sie zu vergrößern oder zu verkleinern seien. Es entstehen Denkweisen wie etwa „Wo keine Nullen sind, werden welche angehängt, wo welche sind, werden sie weggelassen.“ Leider sind diese aber wirklich nur in den erwähnten schematischen Aufgabenblöcken zielführend!
Eine weitere Ursache für Schwierigkeiten beim Umwandeln ist ebenfalls didaktischer Natur (und somit erfreulicherweise leicht aus der Welt zu schaffen): In Anbetracht der vielen mathematischen Voraussetzungen des Umwandelns, wird allgemein viel zu früh damit begonnen! Schon an dieser Stelle plädieren wir daher für ein Aufschieben des Umwandelns auf höhere Klassenstufen. Warum dies ein entscheidender Schritt in Richtung verständiges Lernen wäre, wird deutlicher, wenn wir uns die vielen Voraussetzungen, die es im Vorfeld abzusichern gilt, genauer ansehen.
Würde nicht ab der zweiten Klasse schon (leider oft auch noch dazu sinnentleert) in kleinen Schritten (eben dem kleinen Zahlenraum angepasst) umgewandelt, könnte im Unterreicht Zeit gewonnen werden. Zeit, die für den wichtigen Aufbau von Größenverständnis, für das Sammeln von Handlungserfahrungen zum Messen, sowie für Schätzaktivitäten und Problemaufgaben mit Größen dringend erforderlich wäre.
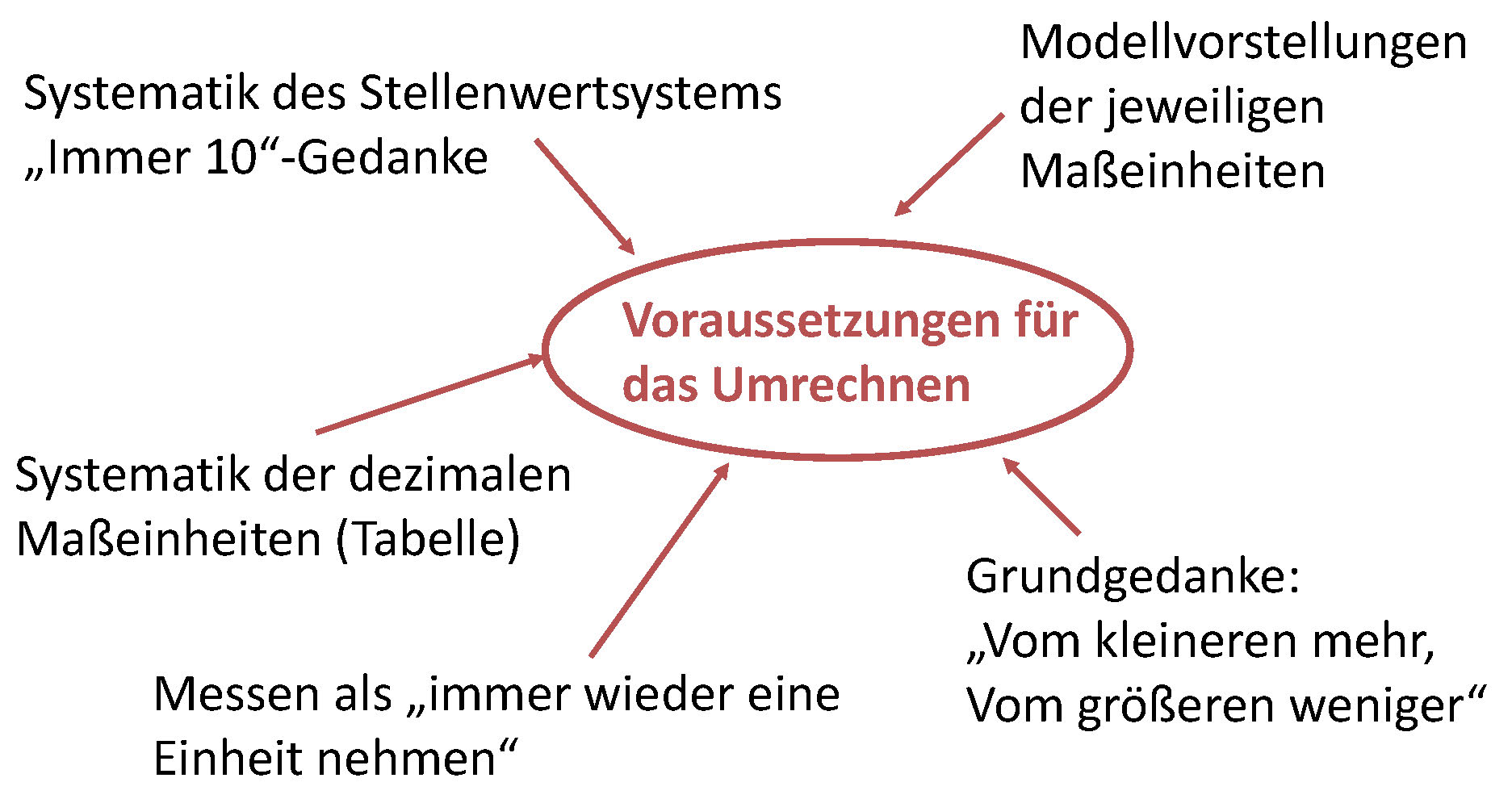
Das Umwandeln der dezimalen Maßeinheiten setzt grundlegende Einsichten in unser Dezimalsystem voraus, die über mehrere Schulstufen hinweg geklärt und gefestigt sein müssen:
Dass die dezimalen Maßeinheiten nach derselben Logik „funktionieren“ wie das dezimale Stellenwertsystem, liegt auf der Hand. Auch hier können jeweils 10 von einer Einheit in die nächstgrößere Einheit umgetauscht werden. Das gemeinsame Prinzip wird deutlicher, wenn der erarbeitete Zahlenraum entsprechend groß ist.
Können Kinder Fragen beantworten wie etwa „wie viele Tausender stecken in einer Million?“ haben sie die Voraussetzung, über einen Zusammenhang von zum Beispiel Kilogramm und Tonnen nachzudenken. Beide Zusammenhänge lassen sich übrigens ohne zu rechnen aus einer Stellentafel oder Maßeinheitentabelle ablesen, wenn die quantitativen Zusammenhänge der einzelnen Spalten verstanden sind.
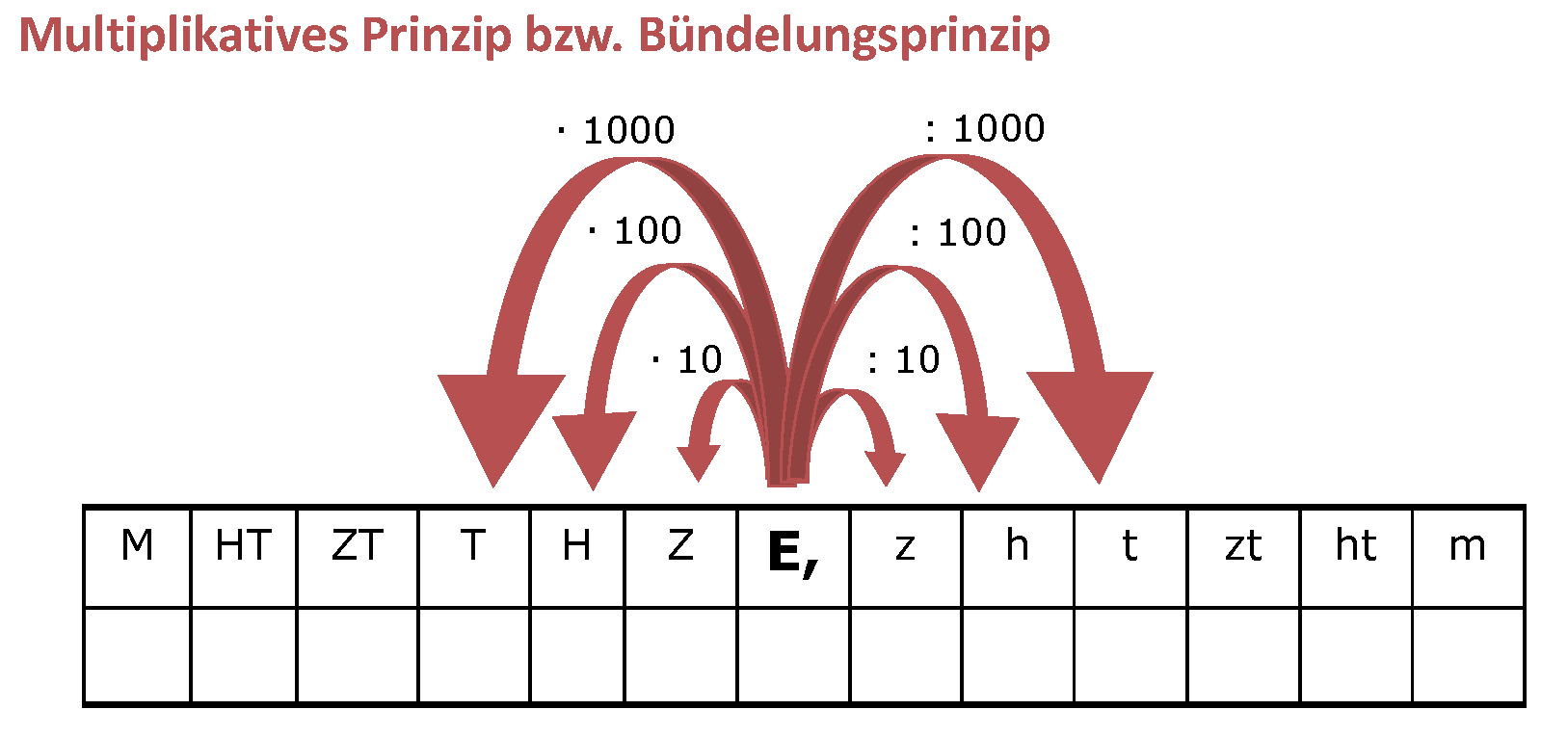
Noch eine Anmerkung zum Vergrößern oder Verkleinern von Stellenwerten: Vor Tipps wie „mal 10 heißt, einfach 1 Null anhängen“ muss schon alleine deshalb gewarnt werden, weil eine prozedurale und unverstandene Befolgung dieses Tipps bei vielen Kindern ab der 5. Schulstufe zu Fehlern im Umgang mit dem Komma führt: 3,5 mal 10 ist eben nicht 3,50 (Null angehängt!), sondern 35!
Der Vorgang des Messens kann und soll – hoffentlich aufbauend auf Grunderfahrungen, die schon im Kindergarten gemacht wurden – ab der ersten Schulstufe gezielt erarbeitet werden.
Nicht wenige Kinder haben nämlich, wenn überhaupt, ein rein äußerliches Verständnis von Messen, etwa in der Weise: „Ich lese am Lineal eine Zahl ab.“ (Oft genug wird dann bereits die Angabe der Maßeinheit als überflüssig empfunden: „Der Tisch ist 80 lang!“ oder auch „Ich bin 35 schwer!“)
„Der Tisch ist 6 Bleistifte lang“: Messen als „immer wieder dieselbe Länge anlegen“
Für das Umwandeln ist aber ein tieferes Verständnis des Messens nötig. Dieses kann am einfachsten im Bereich des Messens von Längen erarbeitet werden, muss aber später auch auf andere Größenbereiche (Gewichte, Flüssigkeitsmengen, Flächen…) übertragen werden.
Im Bereich von Längen lässt sich Messen in etwa so beschreiben: Ich stelle fest, wie oft eine bestimmte, vorher gewählte Länge (die „Maßeinheit“) sich innerhalb der Länge, die ich messen möchte, hintereinander legen lässt; wie oft also diese Einheit „hineinpasst“. Die Maßeinheit ist dabei grundsätzlich frei wählbar. Ich kann eine Länge auch mit nicht-genormten Maßeinheiten ausmessen, z.B. den Schreibtisch mit „Radiergummi-Längen“, das Zimmer mit „großen Schritten“ oder auch „Fußlängen“. Freilich werden viele Kinder bereits Vorerfahrungen zu einigen genormten Maßeinheiten mitbringen, v.a. dem Meter; diese sollen natürlich aufgegriffen und weitergeführt werden.
Bereits an dieser Stelle kann und soll besprochen werden, dass es beim Messen um zwei Dinge geht: die gewählte „Maßeinheit“ und die „Maßzahl“, welche angibt, wie viele solche gleichen Maßeinheiten in die zu messende Länge „hineinpassen“. Wenn ich weiß, dass ein „Zimmer 5 lang ist“, weiß ich gar nichts. „5 Schritte lang“ – das sagt schon um einiges mehr aus; aber sind es 5 große Schritte oder 5 kleine Schritte?
Mit solchen Fragestellungen kann und soll dann auch ein Verständnis dafür erarbeitet werden, warum eindeutig festgelegte, also genormte Einheiten wie „Meter“ oder „Zentimeter“ sinnvoll sind. Diese metrischen Einheiten stehen in weiterer Folge beim Messen im Vordergrund.
Wilhelm Schipper definiert die Lernziele im Umgang mit Größen folgendermaßen: „An erster Stelle geht es um die Entwicklung von Größenvorstellungen … Die mehr technischen Anforderungen des Umwandelns von Größen und des Rechnens mit ihnen sind demgegenüber nachgeordnete Kompetenzerwartungen“ (2009).
Auf Grundlage der oben beschriebenen Messaktivitäten sollte im Unterricht also der Entwicklung von Modellvorstellungen als Basis für Größenvorstellungen bereits früh und vor allem ausreichend Raum gegeben werden. Nach dem Sammeln von Messerfahrungen sollten Kinder – immer noch fern von jedem Umwandeln – Modellvorstellungen zu den wesentlichen Maßeinheiten entwickeln können. Größenvorstellungen entwickeln sich aber nicht von selbst, dafür braucht es entsprechende Aktivitäten.
Tatsache ist, dass viele Schüler*innen, die beim Umwandeln Schwierigkeiten haben, gar keine klaren Vorstellungen davon haben, wie lange denn nun 1 Meter oder 1 Zentimeter ist. (Noch deutlicher sind diese Defizite in der Regel im Bereich der Gewichtsmaße.)
Was hier zu tun wäre, geht über das Herstellen eines Bezugs zum eigenen Körper und das Lernen von „Merksprüchen“ wie „Ein Zentimeter ist so lang, wie ein Fingernagel breit ist“ weit hinaus: Modellvorstellungen prägen sich dadurch ein, dass die metrischen Maßeinheiten immer wieder bewusst verwendet werden. Kinder sollten immer wieder Strecken abmessen, indem sie Zentimeter an Zentimeter reihen (und nicht einfach nur an einem Zentimeterband ablesen); Meter an Meter reihen (und nicht einfach nur an einem Meterband ablesen) …
Und Kinder sollten unbedingt, wenn auch in einem weiteren Schritt, immer wieder dazu angespornt werden, vor dem Messen eigene Schätzungen abzugeben. Fragen wie „Wie viele Meterstäbe, glaubst du, gehen sich bis zur Tür aus?“ „Wie viele Zentimeter-Würfel brauchst du für diesen Bleistift?“ sollen Schätzungen provozieren. Durch nachfolgendes Überprüfen mittels Messung und neuerliches Schätzen weiterer Längen werden einerseits die Schätzfähigkeit geschult, andererseits Modellvorstellungen der Maßeinheiten gefestigt.
Der Grundgedanke des Umwandelns von Maßeinheiten lautet: Von der kleineren Einheit brauche ich zum Messen einer vorgegebenen Größe mehr, von der größeren Einheit weniger. Dieser Grundgedanke lässt sich handelnd aus dem Messen mit unterschiedlichen Einheiten heraus entwickeln: Kinder werden beim Sammeln von Messerfahrungen mit unterschiedlichen Einheiten gemessen haben und dabei bereits – hoffentlich ganz nebenbei – die Erfahrung gemacht haben, dass sich von größeren Einheiten weniger in derselben Strecke ausgehen als von kleineren Einheiten. Diese grundsätzliche Erkenntnis sollte vor dem eigentlichen Umwandeln auch auf andere Maße übertragen und abstrahiert werden können.
Eine entsprechende Übung wäre das Erstellen eines Handlungsprotokolls: Kinder sollen dieselbe Länge (etwa eine Buchkante) einmal mit dm, einmal mit cm abmessen. Wenn dm verwendet werden, benötigt man weniger davon; wenn cm verwendet werden, benötigt es mehr…
„Umwandeln“ ist in seiner Grundform ja nichts anderes als die Überlegung: Wie viele von einer bestimmten Einheit brauche ich zum Abmessen derselben Strecke, die bereits einmal, aber mit einer anderen Einheit abgemessen wurde? Wenn ich dieselbe Strecke zweimal messe, einmal mit einer größeren, dann mit einer kleineren Einheit – dann benötige ich von der kleineren Einheit mehr, umgekehrt von der größeren Einheit weniger. Diese Überlegung sollte durch geeignete Aufgabenstellungen gewissermaßen „automatisiert“ werden: Man könnte diesen Schritt „Umwandeln ohne Zahlen“ nennen.
Einige Anregungen:
Nicht alles, was möglich ist, muss wirklich praktisch ausprobiert werden. Gedankenexperimente sollten reichen, um das verstandene Grundprinzip in den jeweiligen Maßbereich zu übertragen. Ein Beispiel, das ganz ohne Wasser beantwortbar sein sollte: „Wenn wir die Badewanne mit Gläsern ausschöpfen müssen, müssen wir dann öfter schöpfen wenn wir Stamperl benutzen oder wenn wir Krügel benutzen?“ Das allgemeine Prinzip sollte wiederholt festgehalten werden.
Die dezimalen Maßeinheiten sind in völliger Analogie zu den Stellen des Dezimalsystems konstruiert. Diese Analogie kann jedes Kind begreifen, welches auch das Stellenwertsystem begriffen hat. Die folgende Tabelle zeigt das System in der vollen strengen Logik, die ihm seine Erfinder – französische Mathematiker in der Zeit der französischen Revolution – gegeben haben:
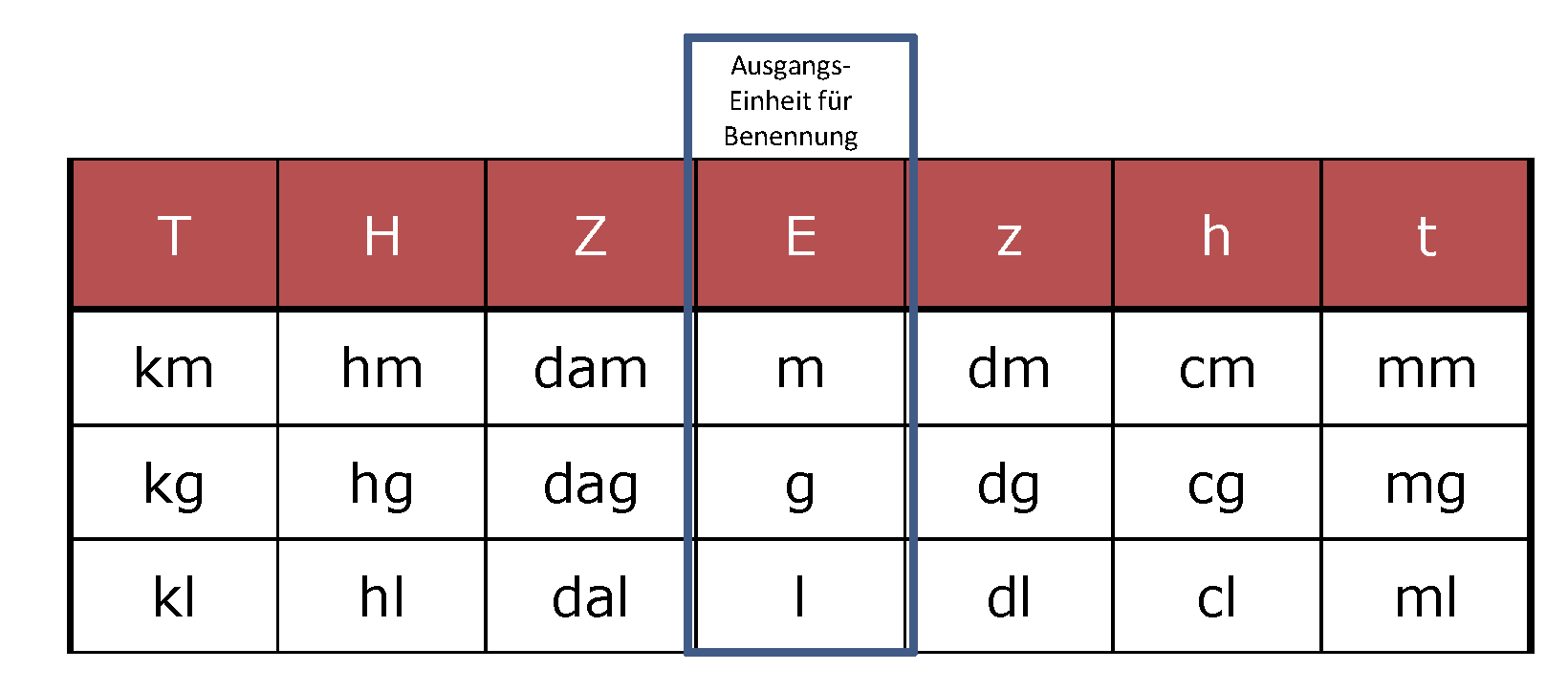
Diese Übersicht zeigt den Vorteil einheitlicher und sinntragender Vorsilben auf. Das aus dem Griechischen entnommene „Kilo“ heißt nichts anderes als 1000, „Hekto“ bedeutet 100, „Deka“ bedeutet 10. Immer, egal ob Meter, Gramm oder Liter als Ausgangseinheit gewählt werden! Analog dazu verhält es sich mit den von lateinischen Zahlwörtern abgeleiteten Vorsilben „Dezi“ für ein Zehntel, „Centi“ für ein Hundertstel und „Milli“ für ein Tausendstel.
Für Kinder mit Stärken im sprachlichen Bereich, aber auch für Erwachsene, die mit Maßen auf Kriegsfuß stehen, kann ein Zugang über die gemeinsamen Vorsilben als übersetzbare Vokabel zu richtigen Aha-Erlebnissen im Verständnis der dezimalen Maßeinheiten führen.
Auch hier gilt: wer erkennt, dass immer das gleiche Prinzip herrscht, tut sich leichter, dieses zu durchschauen und abzuspeichern. In Schulbüchern findet sich eine derartige gemeinsame Übersicht leider nicht. In Grundschulbüchern ist das Gramm die kleinste Gewichtseinheit, Flüssigkeitsmaße finden sich oft gar nicht. Es ist aber um nichts schwerer, Maßtabellen in einer vollständigen und in der Erarbeitungsphase lückenlosen Gegenüberstellung kennenzulernen – im Gegenteil.
In einem weiteren Schritt können die Tabellen auf heute gebräuchliche Maßeinheiten eingeschränkt werden, wobei es je nach Land, beziehungsweise sogar nach Region und auch nach Berufen unterschiedlich sein kann, welche Einheiten gebräuchlich sind und welche nicht.
Dazu einige Denkanstöße: Das in Ostösterreich durchgesetzte Dekagramm ist im Großteil Deutschlands, und auch in Westösterreich nicht gebräuchlich, oft sogar unbekannt. In Italien misst man prosciutto und formaggio in „etto“ – nichts Anderes als „Hektogramm“! Der in Schulbüchern über viele Schuljahre hinweg verwendete Dezimeter findet sich in der Berufswelt gar nicht mehr wieder. Der aus der Zeit der Holzfässer übliche Hektoliter wird in Zeiten riesiger Stahltanks vielleicht einmal durch ein Kiloliter ersetzt?
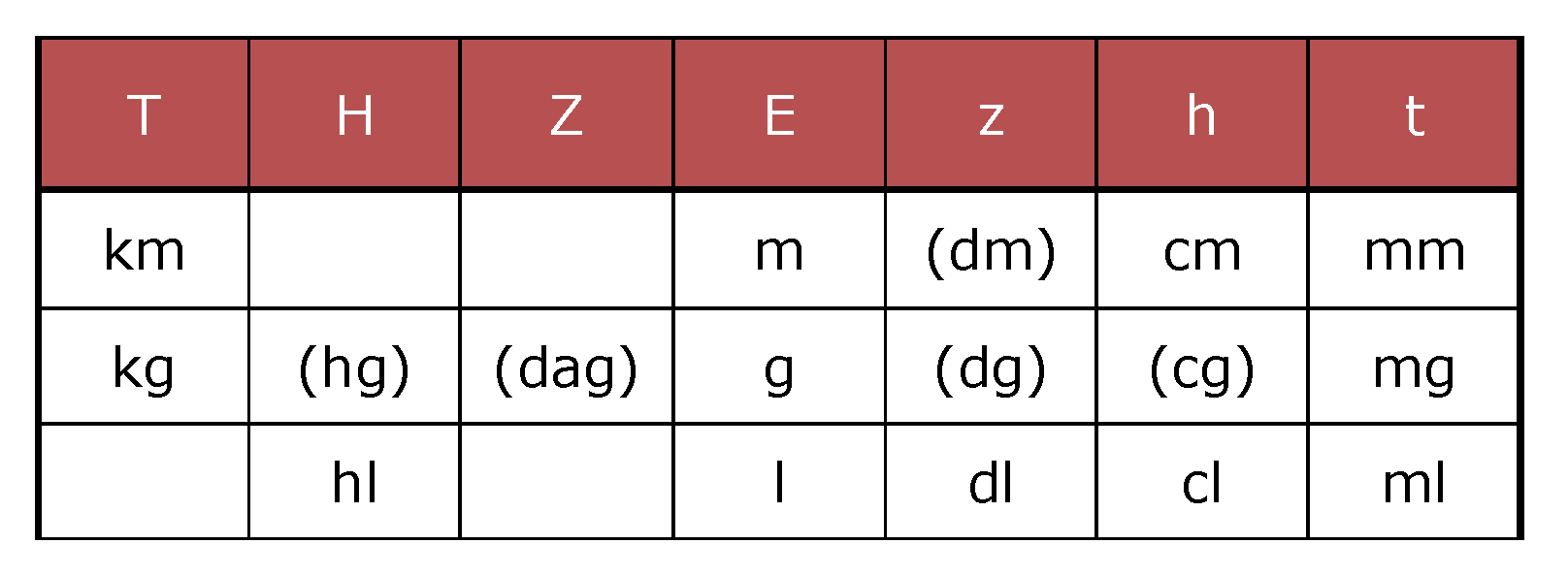
Von besonderer Bedeutung ist es, in einem zweiten Schritt der Erarbeitung der Maßtabellen die „Lücken“ in der Systematik zu besprechen und zu klären.
Ist das bisher Besprochene abgesichert, dann ist es nur noch ein kleiner Schritt zum eigentlichen Umwandeln. Erarbeitet werden sollte ein Schritt-für-Schritt-Vorgehen, bei dem alle bisher erarbeiteten und abgesicherten Voraussetzungen zusammengeführt werden:
In der Kurzfassung klingt das dann bei jeder einzelnen Aufgabe so:
„die Einheit wird kleiner, also wird die Zahl größer, um …. Stellen“
oder eben umgekehrt
„die Einheit wird größer, also wird die Zahl kleiner, um …. Stellen“
Kinder, die wie beschrieben mit Verständnis an Umwandelaufgaben herangehen, können somit nur noch an einer Sache scheitern: nicht sicher zu wissen, um wie viele Stellen sie die Zahlen vergrößern bzw. verkleinern müssen.
Zum sicheren Umwandeln gehört neben dem Verständnis auch das sichere Wissen um die „Umrechnungszahlen“. So lange dieses noch nicht abrufbar ist, spricht nichts dagegen, eine für den jeweiligen Maßbereich erstellte Tabelle der Einheiten als Hilfsmittel verwenden zu lassen. Kinder sollten freilich ermutigt werden, die benötigte Tabelle jeweils (notfalls wiederholt) selbst zu erstellen. Das aktive und wiederholte Reproduzieren der Tabelle wird diese besser im Gedächtnis festigen als das bloße Anschauen einer bereits vorgefertigten. Ein Blick auf die vom Kind erstellte Tabelle kann darüber hinaus auch der Lehrperson Auskunft über mögliche Fehlerquellen geben.
Wie jede mathematische Grundfertigkeit muss auch das Umwandeln durch (je nach Kind unterschiedlich zeitintensive) Übungen automatisiert werden, d.h.: die begriffenen Schritte müssen zur Selbstverständlichkeit werden und ohne großes Grübeln flüssig ablaufen. Mit Blick auf die in vielen Schulbüchern immer noch verbreiteten „Aufgaben-Kolonnen“ muss dabei nochmals vor stereotypen Übungen gewarnt werden: diese führen die Aufmerksamkeit weg von den Maßeinheiten und den hilfreichen Grundüberlegungen und hin zu den Zahlen, und verleiten so zum Abarbeiten unreflektierter Schematismen.
Sowohl im Interesse eines „Einschleifens“ von Schritten, als auch im Interesse einer Kontrolle des tatsächlichen Verständnisses müssen Übungsformate gewählt werden, die eine bloß „mechanische“ Erledigung unmöglich machen.
Für einen verständnisorientierten Unterricht empfiehlt sich folgender didaktischer Aufbau des Themas „Größen“:
In den ersten 3 bis 4 Schuljahren sollte den drei Schwerpunktthemen Messen, Modellvorstellungen und Schätzen ausreichend Zeit gewidmet werden. Im Detail geht es beim Messen um nicht-konventionelle und konventionelle Maßeinheiten, auch darum, Messgeräte kennenzulernen, alles mit dem Ziel, die Messprinzipien zu verstehen. Verschiedene Maßeinheiten untereinander vergleichen und In-Beziehung-bringen ist ein wichtiger Zwischenschritt zum Schätzen (mit Nachmessen) und zum Aufbau von Modellvorstellungen. Auch Problemlöseaufgaben sind unter Nutzung des erarbeiteten Stützpunktwissens möglich und sinnvoll.
Erst wenn der Zahlenraum ausreichend groß ist, mindestens bis Million, idealerweise sogar erst noch nach der Erarbeitung der Dezimalzahlen, und erst wenn ausreichend Messerfahrungen und Schätzaktivitäten gemacht worden sind und darüber Größenvorstellungen erarbeitet sind, ist die Einführung einer tabellarischen Gesamtübersicht über das metrische System sinnvoll. Ab diesem Zeitpunkt ist es dann möglich, „gebräuchliche Größenangaben in unterschiedlichen Schreibweisen darzustellen und in verschiedenen Einheiten anzugeben“ – und das auf Basis von solidem Verständnis.